A binomial probability experiment is conducted with the given parameters, providing a powerful tool for analyzing the probability of success in a sequence of independent trials. This statistical technique finds wide-ranging applications in fields such as quality control, medical research, and social sciences, making it an essential concept in probability theory.
The binomial probability distribution, defined by the number of trials and the probability of success, plays a crucial role in understanding the likelihood of obtaining a specific number of successes in a given experiment. By leveraging this distribution, researchers can model real-world scenarios, make predictions, and draw meaningful conclusions from experimental data.
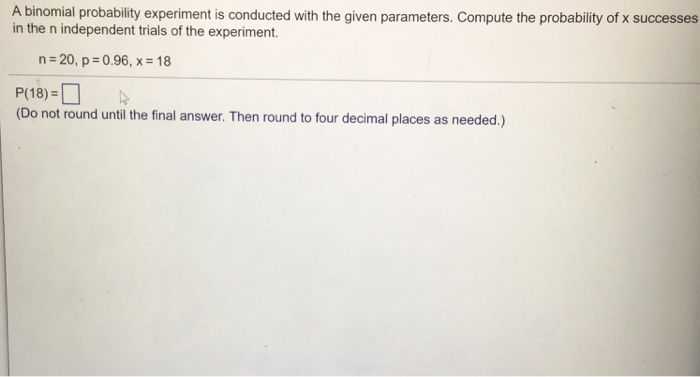
Parameters of a Binomial Probability Experiment: A Binomial Probability Experiment Is Conducted With The Given Parameters
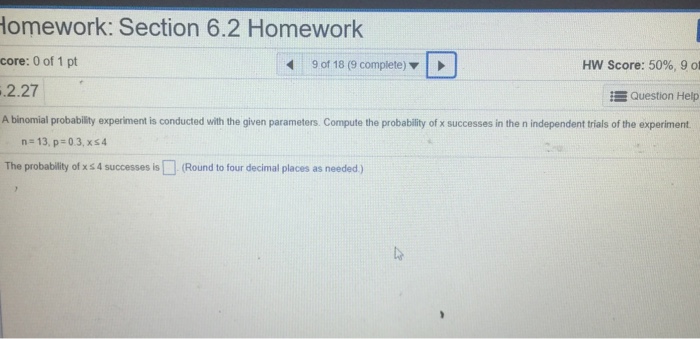
A binomial probability experiment is a statistical experiment that involves a sequence of independent trials, each with a constant probability of success. The parameters of a binomial probability experiment are:
- Number of trials (n):The number of independent trials in the experiment.
- Probability of success (p):The constant probability of success on each trial.
Binomial probability experiments are used to model a wide variety of real-world scenarios, such as the number of heads obtained when flipping a coin multiple times or the number of defective items in a batch of manufactured products.
Probability Distribution of a Binomial Experiment
The probability distribution of a binomial experiment is given by the binomial probability mass function:
P(X = x) = (n choose x)
- p^x
- (1-p)^(n-x)
where:
- X is the random variable representing the number of successes.
- (n choose x) is the binomial coefficient, which represents the number of ways to choose x successes from n trials.
- p is the probability of success on each trial.
- (1-p) is the probability of failure on each trial.
The binomial probability distribution is a discrete probability distribution that describes the probability of obtaining a specific number of successes in a sequence of independent trials.
Applications of Binomial Probability Experiments
Binomial probability experiments are used in a variety of fields, including:
- Quality control:To determine the proportion of defective items in a batch of manufactured products.
- Medicine:To evaluate the effectiveness of a new drug or treatment.
- Marketing:To predict the response rate to a marketing campaign.
- Insurance:To estimate the probability of an event occurring, such as a car accident or a house fire.
Binomial probability distributions are powerful tools for modeling real-world scenarios and making informed decisions.
Limitations of Binomial Probability Experiments, A binomial probability experiment is conducted with the given parameters
Binomial probability experiments are based on the following assumptions:
- The trials are independent.
- The probability of success is constant across all trials.
- The number of trials is fixed.
If these assumptions are not met, then the binomial probability distribution may not be an appropriate model for the experiment.
Popular Questions
What are the key parameters of a binomial probability experiment?
The number of trials (n) and the probability of success (p) are the two key parameters that define a binomial probability experiment.
How is the probability of success in a binomial experiment calculated?
The probability of success in a binomial experiment is calculated using the binomial probability distribution formula: P(X = x) = (n! / (x!(n-x)!)) – p^x – (1-p)^(n-x), where n is the number of trials, x is the number of successes, and p is the probability of success.
What are some common applications of binomial probability experiments?
Binomial probability experiments are widely used in quality control, medical research, social sciences, and other fields where the probability of success in a sequence of independent trials needs to be analyzed.